Programowanie I R – 2023/2024

grupa 1, wtorek 15:15 – 17:00, sala 1.34komp (OKWF, FUW)
Prowadzący: Michał Parniak (USOSweb/info), email: mparniak@fuw.edu.pl
Konsultacje: indywidualnie, pokój 00.51, CeNT I; proszę u umawianie mailowe; możliwe terminy w poniedziałki, środy i piątki.
Dodatkowe informacje: https://www.fuw.edu.pl/~bzglinicki/teaching/p1r/
Wykład: http://glach.wikidot.com/p1r

Zadanie projektowe 1: pdf
Zadania (seria 1) od pozostałych ćwiczeniowców i wykładowcy: pdf1, pdf2, pdf3

Zadanie projektowe 2: pdf – uwaga! ostatnia podmiana miała miejsce 03.06 około 9:40, ze względu na literówkę!
Zadania (seria 2) od pozostałych ćwiczeniowców i wykładowcy: pdf1, pdf2, pdf3, pdf4

Ćwiczenia 1

Zadania (autorstwa B. Zglinickiego): pdf

Konfiguracja git:

mkdir p1r
cd p1r
mkdir cw1
git init
git config --global user.email <email>
git remote add <remote_name> <remote_repo_url> # na przykład git remote add origin https://github.com/OWNER/REPOSITORY.git
git add .
git commit -m "hello world!"
ssh-keygen -t ed25519 -C your_email@example.com* # klucz zostaje wygenerowany w katalogu ~/.ssh/

dodajemy klucz publiczny do Githuba

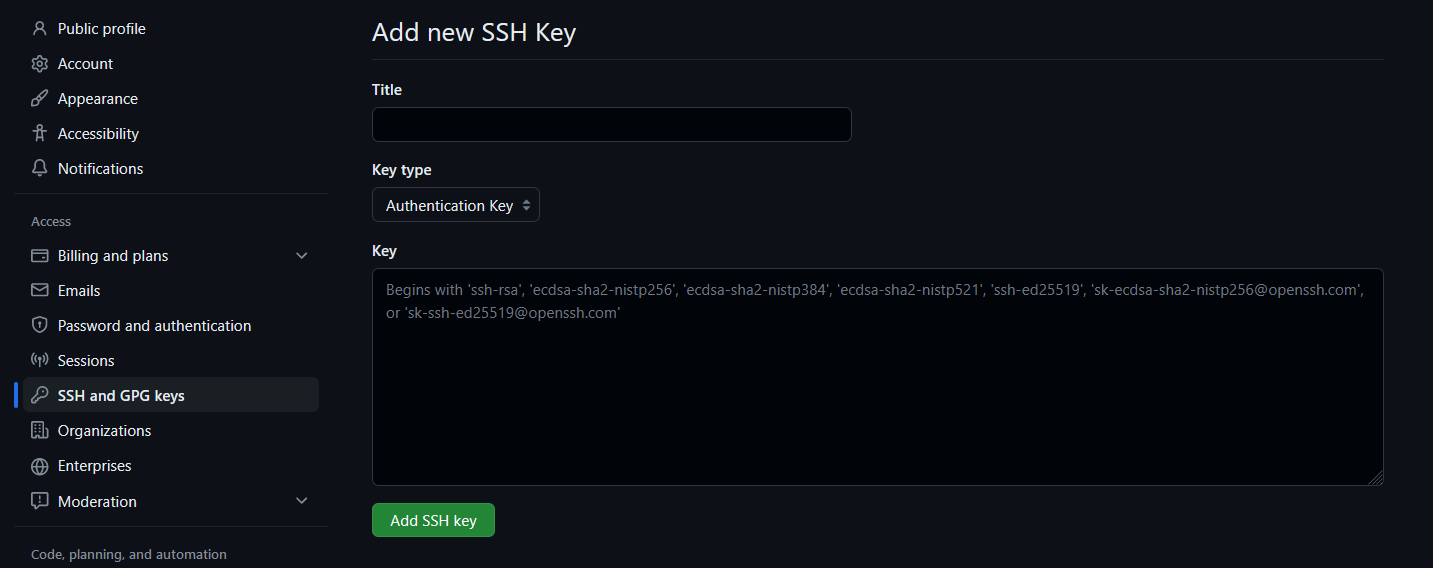
Na koniec, aby wysłać na serwer:

git push origin master

Ćwiczenia 2

Zadania (autorstwa B. Zglinickiego): pdf

Ćwiczenia 3

Zadania (autorstwa B. Zglinickiego): pdf

Ćwiczenia 4

Zadania (autorstwa B. Zglinickiego): pdf

Ćwiczenia 5

Zadania (autorstwa B. Zglinickiego): pdf

Ćwiczenia 6

Zadania (autorstwa B. Zglinickiego): pdf

Ćwiczenia 7

Zadania (autorstwa B. Zglinickiego): pdf

Ćwiczenia 8

Zadania (autorstwa B. Zglinickiego): pdf

Ćwiczenia 10

Zadania (autorstwa B. Zglinickiego): pdf

Zadanie 3 – ball volume

import numpy
import matplotlib.pyplot as plt
def ball_volume(n,N):
    x=np.random.uniform(-1,1,size=[n,N])
    r=np.sqrt(np.sum(x**2, axis=0))
    ile=np.sum(r<=1)
    return ile*(2**n)/N
print(ball_volume(1,1000))

k=15 # Do jakiego wymiaru? 
n=100000 # ile punktów?
volumes=[]
for i in range(k):
    volumes.append(sum([ball_volume(i+1,n) for s in range(5)])/5)
wymiary=[i+1 for i in range(k)]
plt.plot(wymiary,volumes,'s')
plt.show()

Ćwiczenia 11

Zadania (autorstwa B. Zglinickiego): pdf

Zadanie 1 – rozwiązanie przy pomocy funkcji odeint

import numpy as np
from scipy.integrate import odeint
from matplotlib import pyplot as plt

y0= [0,1.1]
t=np.linspace(0,100,10000)

def dy_dt(y, t, a):
    dx0_dt = y[1]
    dx1_dt = -a* np.sin(y[0])
    return np.array([dx0_dt, dx1_dt])

a=1
args = (a,)
yout = odeint(dy_dt, y0, t, args)


plt.plot(t, yout)

Zadanie 1 – rozwiązanie przy pomocy własnej implementacji metody całkowania (w tym przypadku Runge-Kutta 4ego rzędu)

import numpy as np
from matplotlib import pyplot as plt

def dy_dt(y, t, a):
    dx0_dt = y[1]
    dx1_dt = -a* np.sin(y[0])
    return np.array([dx0_dt, dx1_dt])

y0= [0,1.8]
T = np.linspace(0,100,10000)
h = T[1] - T[0]
Y = np.zeros(shape=(2,len(T)))
Yrk = np.zeros(shape=(2,len(T)))
Y[:,0] = y0
Yrk[:,0] = y0
tt = 0
for n in range(len(T)-1):
    tt += h
    Y[:,n+1] = Y[:,n] + h*dy_dt(Y[:,n], tt, a)
    k1 = dy_dt(Yrk[:,n], tt, a)
    k2 = dy_dt(Yrk[:,n]+h*k1/2, tt+h/2, a)
    k3 = dy_dt(Yrk[:,n]+h*k2/2, tt+h/2, a)
    k4 = dy_dt(Yrk[:,n]+h*k3, tt+h, a)
    Yrk[:,n+1] = Yrk[:,n] + h/6*(k1+2*k2+2*k3+k4)
#%% wykres w czasie
plt.plot(T, Yrk[0,:])
plt.plot(T, Yrk[1,:])
#%% wykres w przestrzeni fazowej
plt.plot(Yrk[0,:], Yrk[1,:])

Ćwiczenia 12

Zadania (autorstwa B. Zglinickiego): pdf

Zadanie 1 – rozwiązanie uproszczone do jednego wymiaru, obserwujemy rozpływanie się (dyfuzję) ciepła

#%%
import numpy as np
#from scipy.integrate import odeint
from matplotlib import pyplot as plt


nx=100
X=np.linspace(0,1,nx)
dx=X[1]-X[0]

nt=100
T=np.linspace(0,.001,nt)
h=T[1]-T[0]

psi=np.zeros(shape=(nt,nx))
#%% przykładowe warunki początkowe

#psi[0,:]=np.exp(-(T-T[-1]/2)**2/(10*h)**2)
psi[0,40:60] = 1
#%%

def dy_dt(y, t, alpha):
    # finite-difference estymacja drugiej pochodnej (czyli laplasjanu przestrzennego)
    return alpha*(np.roll(y,1)+np.roll(y,-1)-2*y)/dx**2

alpha=3
tt=0

for n in range(nt-1):
    tt += h
    # metoda Eulera - gorsza
    # psi[n+1,:] = psi[n,:] + h*dy_dt(psi[n,:], tt, alpha)
    # metoda RK4  - lepsza
    k1 = dy_dt(psi[n,:], tt, alpha)
    k2 = dy_dt(psi[n,:]+h*k1/2, tt+h/2, alpha)
    k3 = dy_dt(psi[n,:]+h*k2/2, tt+h/2, alpha)
    k4 = dy_dt(psi[n,:]+h*k3, tt+h, alpha)
    psi[n+1,:] = psi[n,:] + h/6*(k1+2*k2+2*k3+k4)
#%%
plt.plot(T,psi[0,:])
# %%
Tm,Xm=np.meshgrid(T,X)
plt.pcolormesh(T,X,np.abs(psi)**2)
# %%

Ćwiczenia 13

Zadania: pdf

Zadania dodatkowe (z innej grupy): pdf

Zadanie 1; obrazek testowy: snail.bmp

#%%
from PIL import Image
img = Image.open('snail.bmp').convert('L')
#%%
import numpy as np
arr_img=np.array(img)
# %%
from matplotlib import pyplot as plt
plt.imshow(arr_img,cmap="Greys_r")
# %% ogladanie fft
fft_img=np.fft.fft2(arr_img)
fft_img=np.fft.fftshift(fft_img)
fft_img_logscale = np.log10(np.abs(fft_img)**2)
plt.imshow(fft_img_logscale)
# %% aplikacja filtra
x, y = arr_img.shape
sigma=50
fft_img[0:x//2-sigma,:]=0
fft_img[x//2+sigma:,:]=0
fft_img[:,0:y//2-sigma]=0
fft_img[:,y//2+sigma:]=0
fft_img_logscale = np.log10(np.abs(fft_img)**2)
plt.imshow(fft_img_logscale)
# %% ifft
new_img = np.fft.ifft2(np.fft.ifftshift(fft_img))
plt.imshow(np.abs(new_img),cmap="Greys_r")
# %%

Zadanie 2 – uproszczone, proces Wienera

import numpy as np
from matplotlib import pyplot as plt

T=1000
sigma=1
n=100
psds=[]
for i in range(n):
    dW=np.random.normal(0,sigma,size=T)
    x=np.cumsum(dW)
    trace_fft = np.fft.fft(x)
    trace_fft = np.fft.fftshift(trace_fft)
    psds.append(np.abs(trace_fft)**2)
psd=np.mean(psds,axis=0)
plt.plot(np.log10(psd))

Zadanie 3

#%%
import numpy as np
from matplotlib import pyplot as plt
T=1000
sigma=1
dW=np.random.normal(0,sigma,size=T)
x=np.cumsum(dW)
dW=np.random.normal(0,sigma,size=T)
y=np.cumsum(dW)
plt.plot(x)
plt.plot(y)
# %%
tt=np.arange(T)
omega=0.2
A=(x+1j*y)*np.exp(1j*omega*tt)
S=np.real(A)
plt.plot(S)
# %%
s_fft = np.fft.fft(S)
s_fft = np.fft.fftshift(s_fft)
s_fft[0:T//2]=0
ss=np.fft.ifft(np.fft.ifftshift(s_fft))
#plt.plot(np.abs(s_fft))
ss=ss/np.exp(1j*omega*tt)
plt.plot(np.real(ss))
plt.plot(np.imag(ss))
plt.plot(x/2)
plt.plot(y/2)
# %%

Zadanie 4 – generacja hologramu

#%%
from PIL import Image
img = Image.open('snail.bmp').convert('L')
#%%
import numpy as np
arr_img=np.array(img)
#%%
x,y=arr_img.shape
X=np.arange(x)
Y=np.arange(y)
xx,yy=np.meshgrid(X,Y)
#hologram=np.ones(shape=arr_img.shape)*np.exp(0.00001*1j*(xx+yy**2-xx*yy**2))
hologram=np.array(arr_img,dtype=float)*np.exp(0.00001*1j*(xx+yy**2-xx*yy**2))
# %%
plt.imshow(np.angle(hologram))

Ćwiczenia 14

Zadania: pdf